CyrusBeck参数化裁剪算法基于opengl的实现教程

Cyrus Beck裁剪算法是计算机图形学中的一个实验，这个实验的难点在于理解，而不在于实现。这个算法也是基础算法里比较有趣的一个。CB算法只针对凸多边形，对于凹多边形不适用。

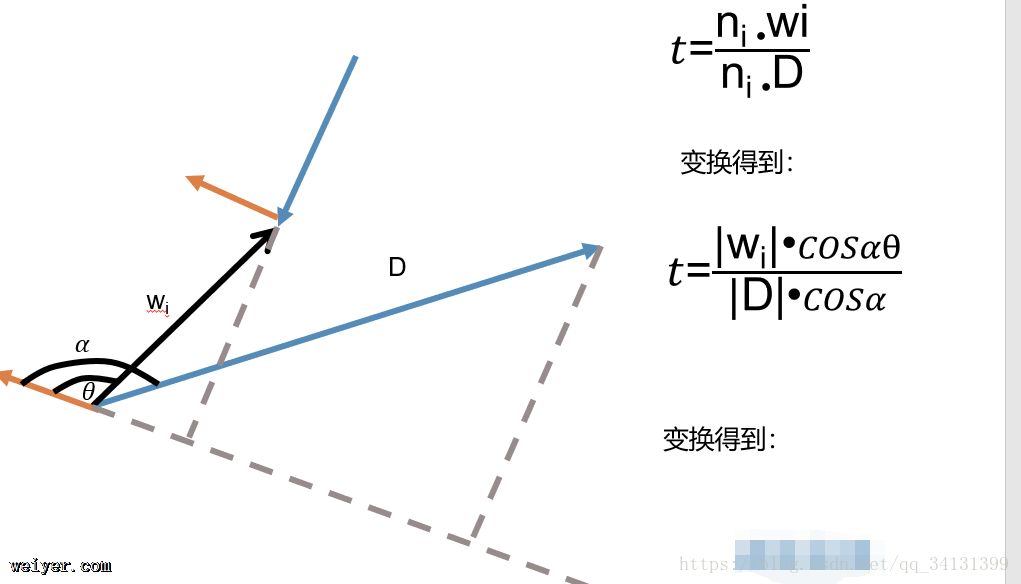
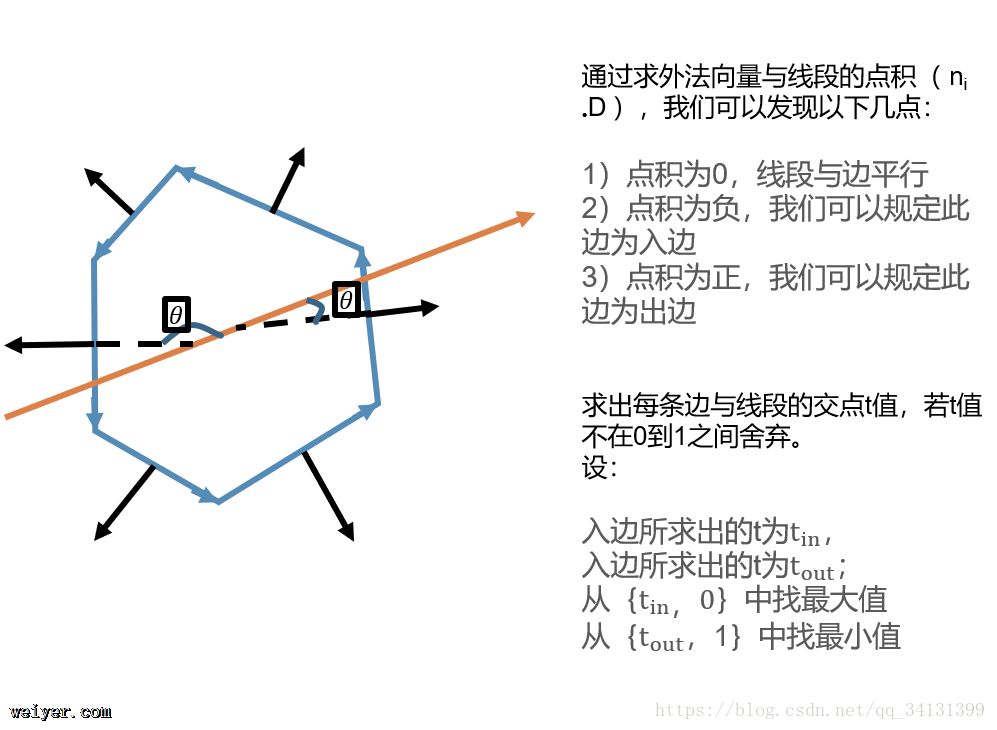
Cyrus Beck算法要求我们对多边形的每条边进行讨论，从而找出真正的入点和出点。CB算法也叫参数化裁剪，那是因为其中用到了初中的几何原理，相似三角形，如果你将实验用到的几个矢量进行简单的平移延长就能发现所谓的参数就是线段之间的比例而已。

Cyrus Beck算法实现一般分为三步

1.求得线的矢量、求每一条边法矢量（要统一为内法矢 或者 外法矢）。

2.求得当前遍历到的多边形边的法矢与线矢量的积，确定这条边是入边还是出边

3.确定了出入，将求得的参数放到已有的参数中比较大小

以下是一个实现步骤

具体的看代码，下面调用了几个简单的求矢量的函数。

//参数化的裁剪算法@
void CB_CilpLine(int idex) {

float tin=0,tout=1;//设置初始tin tout
float curt = -1;//用来记录当前得到的t值

float vectProtVal = 0;//记录法向量和线的点积


gdPointDis2f curPVect;//多边形边的法向量
gdPointDis curLVect;//直线的向量
gdPointDis curLPVect;

//当前直线的向量
curLVect = GetVect(gdLDArr[idex].x0, gdLDArr[idex].y0, gdLDArr[idex].x1, gdLDArr[idex].y1);


int gdPDLength = gdPD.length;
int i = 0;

for (i = 0; i < gdPDLength; i++)
{
//当前多边形 循环到的一边的法向量
curPVect = GetNormalVect(gdPD.pointArr[i].x, gdPD.pointArr[i].y, gdPD.pointArr[(i + 1) % gdPDLength].x, gdPD.pointArr[(i+1)%gdPDLength].y);
//线到多边形边的矢量
curLPVect = GetVect(gdLDArr[idex].x0, gdLDArr[idex].y0, gdPD.pointArr[i].x, gdPD.pointArr[i].y);
 
//获得线和法向量的点积
vectProtVal = GetVectProd2f(curPVect, curLVect);

if (vectProtVal == 0)
{//若点积为零 判为平行 不处理
continue;
}

//求得当前t值 (wi*ni)/(D*ni) 由于用外法矢 就不加负号
curt = GetVectProd2f(curPVect, curLPVect) / vectProtVal;

//由符号判断取值
if(vectProtVal<0)
{
tin = curt > tin  curt : tin;
}
else {
tout = curt < tout  curt : tout;
}

if (tin>=tout)
{//当线在多边形外
gdLDArr[idex].x0 = 0;
gdLDArr[idex].y0 = 0;
gdLDArr[idex].x1 = 0;
gdLDArr[idex].y1 = 0;
return;
}
}

//坐标转换
int dx = gdLDArr[idex].x1 - gdLDArr[idex].x0;
int dy = gdLDArr[idex].y1 - gdLDArr[idex].y0;
int x0, x1, y0, y1;

x0 = dx*tin+ gdLDArr[idex].x0;
y0 = dy*tin+ gdLDArr[idex].y0;
x1 = dx*tout + gdLDArr[idex].x0;
y1 = dy*tout + gdLDArr[idex].y0;

gdLDArr[idex].x0 = x0;
gdLDArr[idex].y0 = y0;
gdLDArr[idex].x1 = x1;
gdLDArr[idex].y1 = y1;
return;
}