网图和非网图中，最短路径的含义不同：

非网图中，因为没有边上的权值，最短路径指的是两顶点之间经过的边数最少的路径； 网图中，最短路径指的是两顶点之间经过的边上权值之和最少的路径，并且称路径上的第一个顶点是源点，最后一个顶点是终点。

迪杰斯特拉（Dijkstra）算法

定义

Dijkstra(迪杰斯特拉)算法是单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。

特点

以起始点为中心向外层层扩展，直到扩展到终点为止。

基本思想

假设 G=(V,{E}) 是一个带权有向图，把图中顶点集合 V 分成两组，

第一组为已求出最短路径的顶点集合 S 及其路径长度（初始时 S 中只有一个源点，以后每求得一条最短路径 , 就加入到集合 S 中，直到全部顶点都加入到 S 中） 第二组为未确定最短路径的顶点集合 U 及其路径长度，按最短路径长度递增次序依次把 U 中的点加入 S 中。在加入的过程中，总保持从源点 v 到 S 中各顶点的最短路径长度不大于从源点 v 到 U 中任何顶点的最短路径长度。

此外，每个点对应一个距离，S 中点的路径长度就是从 v 到这个点的最短路径长度，U 中的点的路径长度，是从 v 到这个点由 S 中的顶点作为中间顶点的当前最短路径长度。

迪杰特斯拉算法不是一下子求出源点到其余各点的最短路径，而是一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到结果。

算法步骤

初始时，S 只包含源点，即 S＝{v}，v 的距离为 0。U 包含除 v 外的其他顶点，即：U={其余顶点}，若 v 与 U 中顶点 u 有边，则 正常有权值，若 u 不是 v 的邻接点，则 权值为 ∞。 从 U 中选取一个距离 v 最小的顶点 k，把 k加入 S 中（该选定的距离就是 v 到 k 的最短路径长度）。 以 k 为新考虑的中间点，修改 U 中各顶点的距离；若从源点v 到顶点 u 的距离（经过顶点 k）比原来距离（不经过顶点k）短，则修改顶点 u 的距离值，修改后的距离值的顶点 k 的距离加上边上的权。 重复步骤 2 和 3 直到所有顶点都包含在 S 中。

算法实例

给出一个无向图：

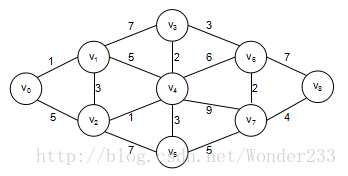
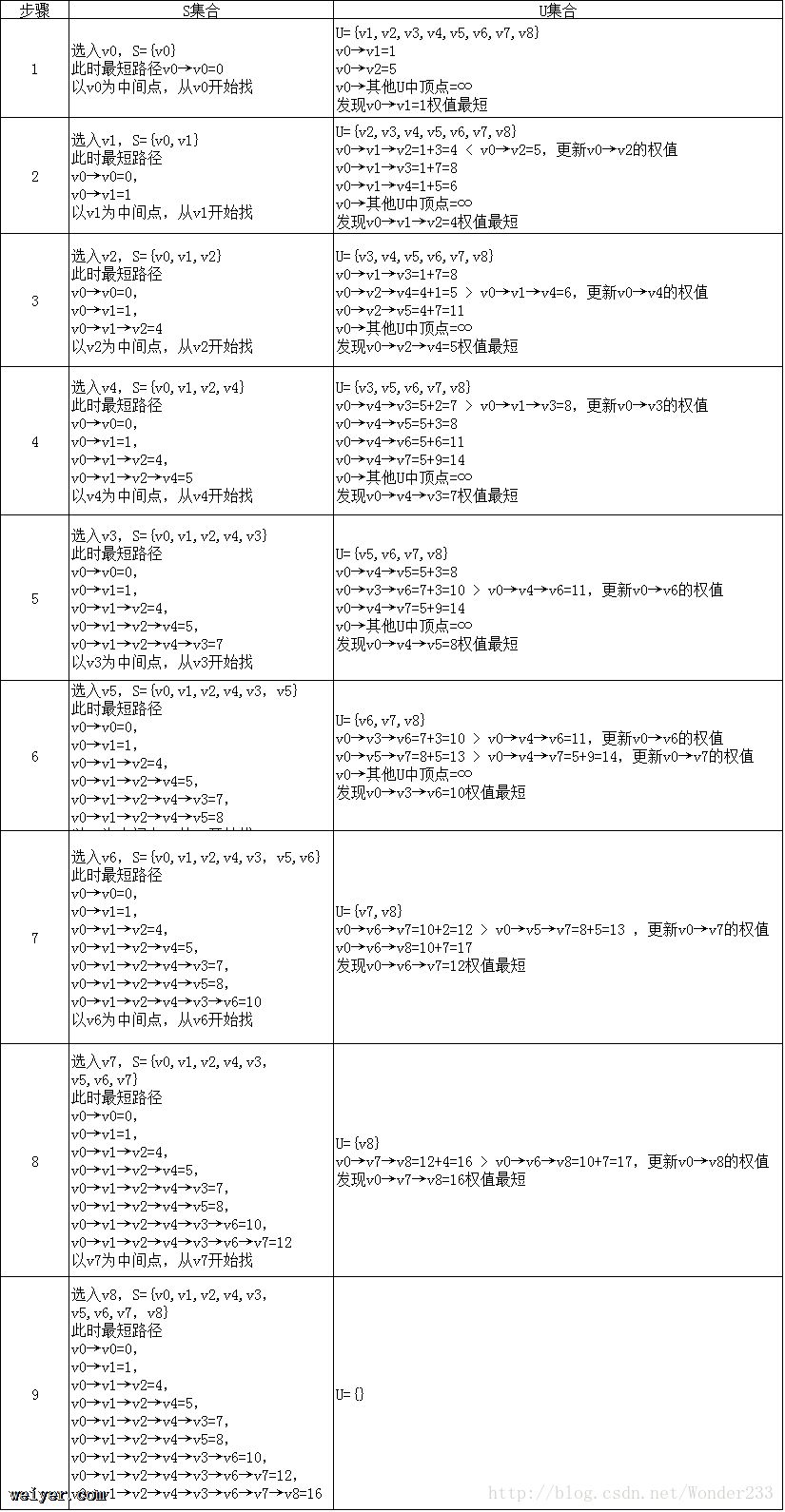
用Dijkstra算法找出以 v0 为起点的单源最短路径步骤如下：