核心提示:1.向量加减 2.向量点积 也称为数量积,其结果为一个标量,其定义为 几何意义: 用于计算两个向量之间的夹角 ab0 方向基本相同,夹角在0到90之间? ab=0 正交(垂直) ab0 方向基本相反,...
1.向量加减
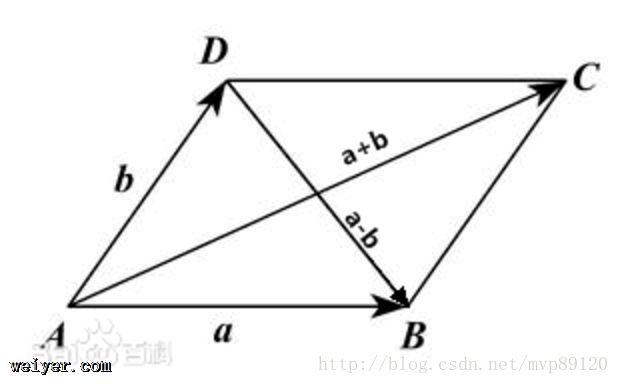
2.向量点积 也称为数量积,其结果为一个标量,其定义为
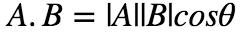
几何意义: 用于计算两个向量之间的夹角 a·b>0 方向基本相同,夹角在0°到90°之间? a·b=0 正交(垂直) a·b<0 方向基本相反,夹角在90°到180°之间 另外也用于计算投影,投影计算得到一个标量 向量A在B上的投影定义为:
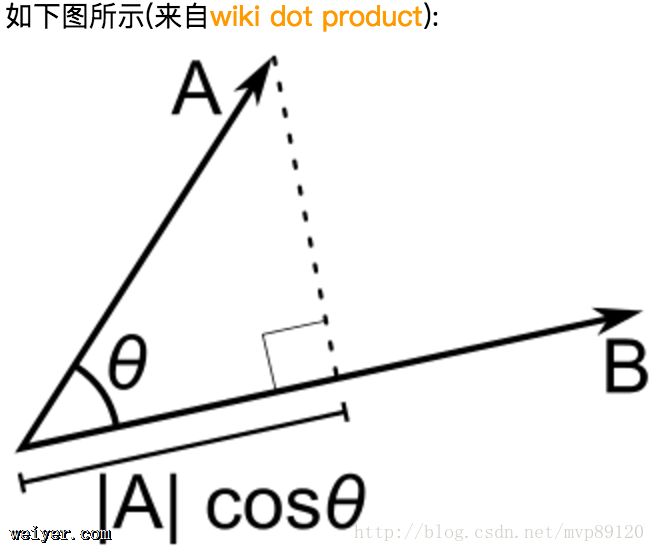
则AB = A.B / |B|
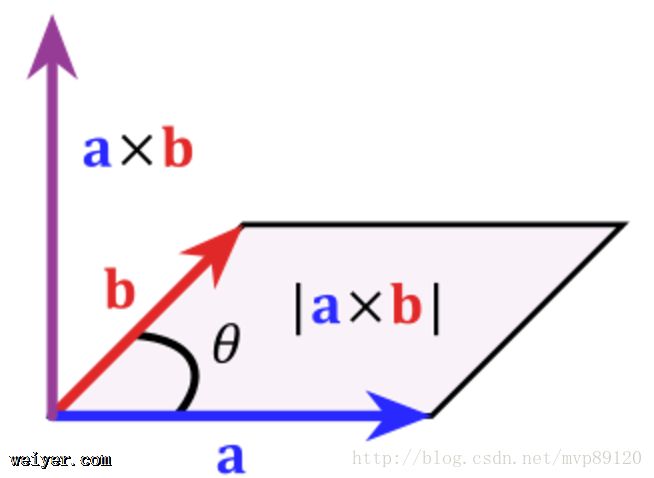
3.向量叉积 两个向量a和b的叉积,结果是一个向量c=a×b,c的方向垂直于a和b,它需要根据右手规则来确定 c的大小等于 |c|=|a||b|sinθ 注意c的方向需要根据右手规则来确定。所谓右手规则是指,将向量a与b放在同一个起点时,当右手的四个手指从a所指方向转到b所指方向握拳时,大拇指的指向即为a×b的方向。
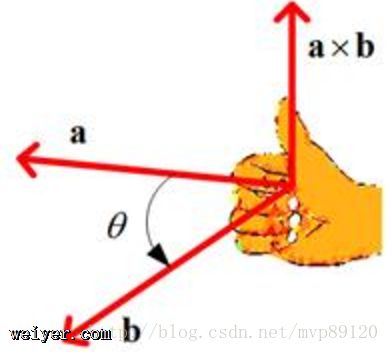
叉积的模可以视为以a和b为两边的平行四边形的面积
4.逆矩阵 对于n阶方阵A,如果存在一个n阶方阵B使得: AB=BA=I (单位矩阵I是主对角线上元素为1,其余元素都为0的n阶方阵) 则称B是A的逆矩阵 在3D图形处理中,用一个变换矩阵乘以向量,代表了对原始图形进行了某种变换,例如缩小,旋转等,逆矩阵表示这个操作的逆操作,也就是能够撤销这一操作。
5.左手坐标系和右手坐标系
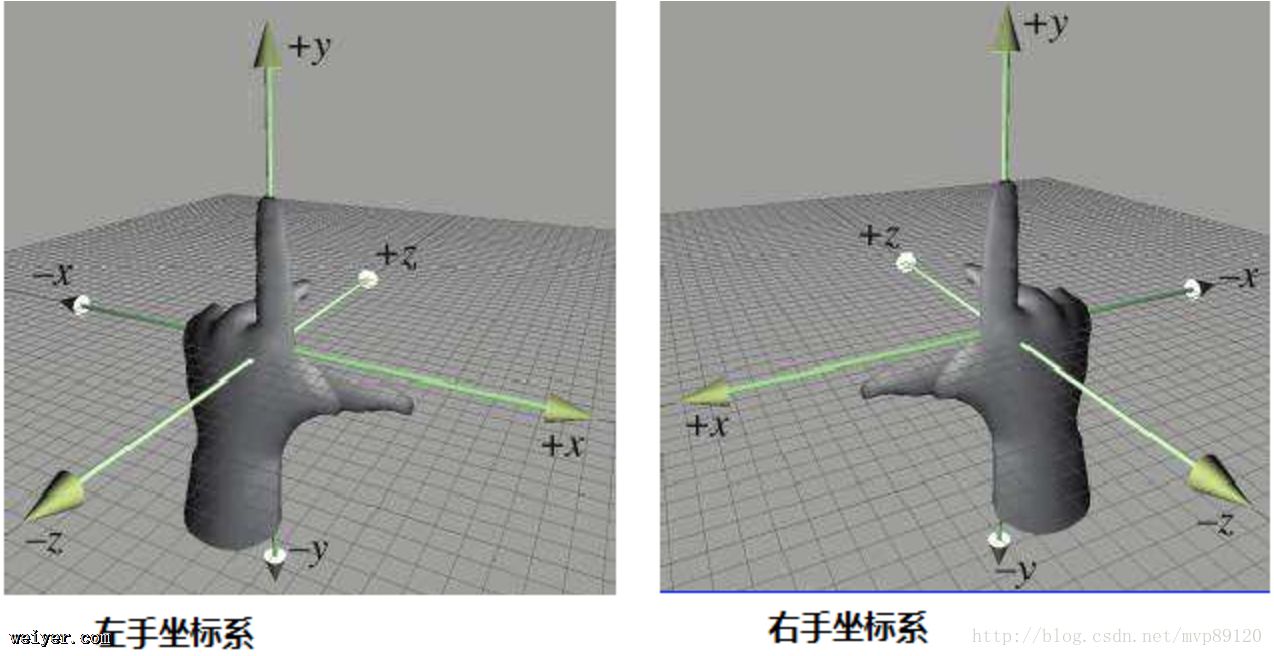
OpenGL中的物体、世界、照相机坐标系都属于右手坐标系,而规范化设备坐标系使用左手坐标系。
6.坐标系 一般地使用的3D笛卡尔坐标系使用标准基向量和坐标原点

因此可以将上述向量组表现为矩阵的形式,任意的坐标位置乘以该矩阵,就可以得到该坐标在该坐标系中的位置或其他变换。